Myths about exploding gradients
Why tanh activation functions lead to exploding, not vanishing, gradients and other things your deep learning textbook probably got wrong
Author’s note: I’m looking for a job in the Bay Area. If you’re interested in hiring me, send me an email at mcgreivy@alumni.princeton.edu or a message on X.
In neural networks, the gradient explodes (or vanishes) when its magnitude repeatedly grows (or shrinks) between layers during backpropagation. To illustrate, consider a simple multi-layer perceptron (MLP) with ReLU activation functions.
If the randomly initialized weights are too large, the weight gradients explode as the weight matrices are repeatedly multiplied together during the backwards pass. If the initial weights are too small, the weight gradients vanish for the same reason. Using sigmoid or tanh activation functions instead of ReLU can also lead to vanishing gradients, because for large inputs their derivatives saturate towards zero.
The above paragraph is consistent with what is usually presented about exploding and vanishing gradients in textbooks, on Wikipedia, by LLMs, and in courses at top universities. Every sentence in the above paragraph, however, is incorrect.
For example, it’s common knowledge that the tanh activation function leads to vanishing gradients, because it “squashes” the input leading to a small derivative.
But in an MLP, tanh activation functions actually lead to exploding, not vanishing, gradients.
This isn’t the only myth about exploding/vanishing gradients. As we’ll see in the rest of this post, one of the most fundamental topics in deep learning is widely misunderstood.
Myth #1: Weight gradients explode or vanish without proper initialization
As any student of deep learning knows, if the weights in a neural network are initialized to have too high or too low variance, then the network will have exploding or vanishing gradients.
But is this actually true? To test, I ran a simple experiment.
The details of the experiment are as follows. I computed the standard deviation of the gradients of the softmax cross-entropy loss with respect to the initial weights1 in a 5-layer MLP with 64 hidden units and ReLU activation functions using a single batch of MNIST data for five different values of the weight initialization “gain” factor: [100, 10, 1, 0.1, 0.01]. A gain of 1 equals the Kaiming normal initialization, while gains of 100, 10, 1, 0.1, and 0.01 result in proportionally higher or lower initial weight variance. The code can be found here.
The standard deviations of the weight gradients at each layer in the MLP are plotted below.
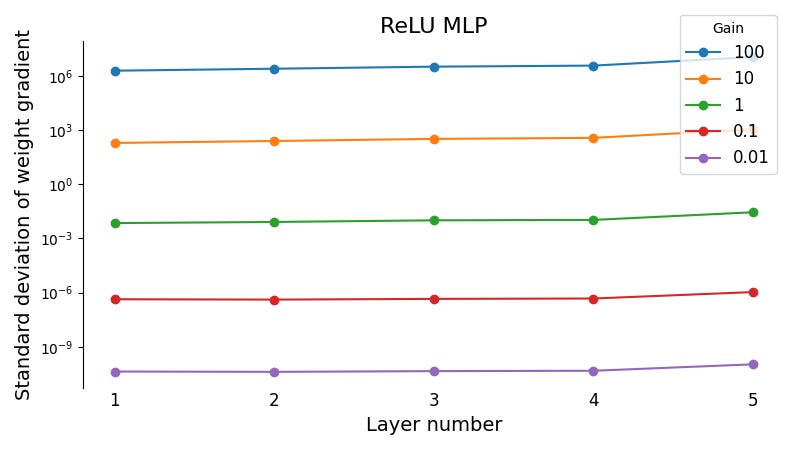
As we can see, the weight gradients neither explode nor vanish. Though they differ in magnitude depending on the scale of the initial weights, the weight gradient variance is in fact constant between layers.
To understand this surprising result, we’ll return to the standard textbook explanation for exploding and vanishing gradients, and consider what it’s missing.
An MLP with L layers and activation function σ can be written as
For simplicity, we’ll assume linear activation functions and initialize the biases to zero. The initial gradient of the loss with respect to the ℓth weight matrix is given by
Purportedly, this matrix chain product is what leads to exploding (or vanishing) gradients in the backwards pass. However, notice that the gradient is given by the outer product of this matrix chain product with the activation.
What most explanations fail to point out is that the activations are also given by a matrix chain product, specifically
Plugging this back into the weight gradient, we have
which scales as 𝒪(||W||L-1).2 This is independent of ℓ, which means that the gradient has approximately constant magnitude across the network as seen in the figure above.
The intuition here is that you’re multiplying a vector which is exploding (or vanishing) in the backwards direction by a vector which is exploding (or vanishing) in the forwards direction, and the two effects cancel out.
So far we’ve looked at the gradients of the weights, not the biases. Here’s the same plot, except for the bias gradients:
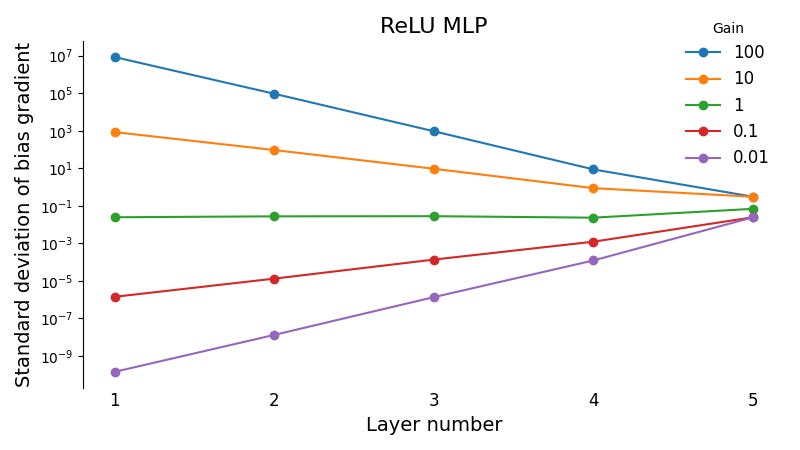
Now we see exploding gradients for gain factors greater than 1, and vanishing gradients for gain factors less than 1. This makes intuitive sense: the bias gradient doesn’t involve multiplying by the activation, so there’s no cancellation.
You might be asking: who cares? After all, even if only the bias gradients explode, that’s still a problem. I still need to initialize the weights from the right distribution to prevent exploding and vanishing bias gradients as well as numerical overflow and underflow. And in an RNN or a transformer, the story will be different in important ways.
This is all true. From the perspective of how to initialize the weights of a neural network, it makes no difference whether it’s the weights or the biases or both that explode.
But theoretically, the distinction can be important. For example, mistakenly thinking that the weight gradients explode contributes to our next myth.
Myth #2: Exploding activations lead to exploding gradients
In a 2017 paper “The exploding gradient problem demystified”, George Philipp and co-authors write:
It has become a common notion that techniques such as introducing normalization layers… or careful initial scaling of weights… largely eliminate exploding gradients by stabilizing forward activations. This notion was espoused in landmark papers.
I haven’t seen any textbooks repeating this notion. However, the idea seems to be common enough that every LLM I asked (except Claude Opus 4.1) agreed that exploding activations cause exploding gradients.
But as we saw in the previous section, exploding and vanishing activations actually prevent exploding and vanishing weight gradients, at least in MLPs. And they have no effect on the bias gradients.
Myth #3: Tanh activation functions cause vanishing gradients
One of the first things taught to every student of deep learning is that sigmoid and tanh activation functions cause vanishing gradients.
But tanh activation functions don’t cause vanishing gradients, and can actually cause exploding gradients.
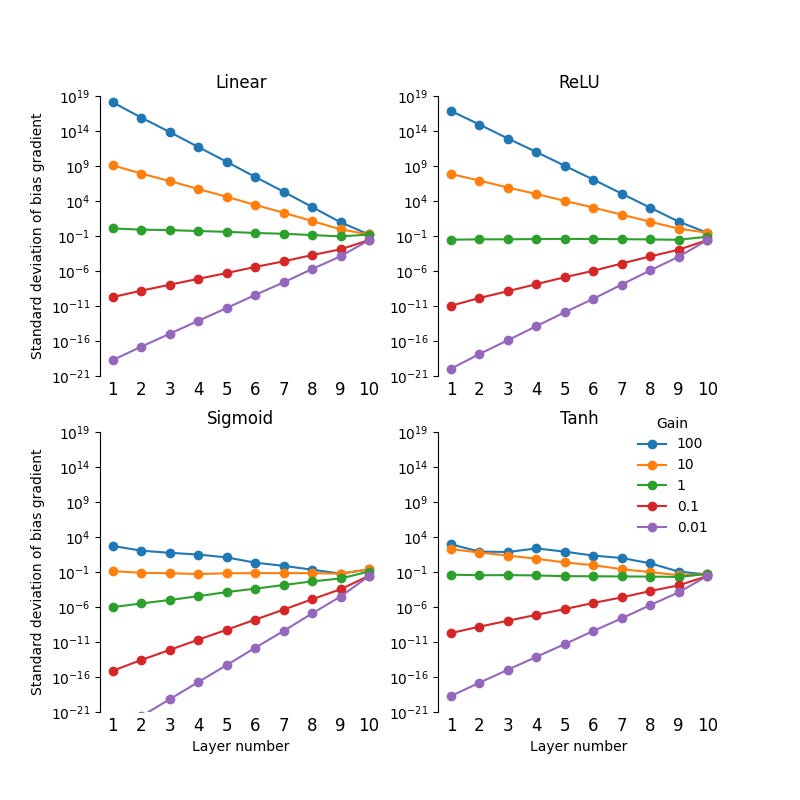
To demonstrate this counterintuitive result, I repeated the earlier experiment for four types of activation functions: linear, ReLU, sigmoid, and tanh. I also increased the number of layers from five to ten. The code can be found here.
The standard deviations of the initial weight gradients at each layer in the MLP for each of the four activation functions are shown below.
As we can see, tanh activation functions lead to exploding weight gradients for gain factors larger than 1.
This happens because the output of the tanh function is between -1 and 1, which prevents exploding activations. But as we know, exploding activations prevent exploding gradients. So by removing the possibility of exploding activations, the tanh activation function allows the gradients to explode if the weight matrices are large.
Another way to think about it is that as we increase the gain factor, the weight matrices W become larger but the derivative of tanh, σ'(x), decreases towards zero. In the backwards pass, as W and σ'(x) are repeatedly multiplied, the effect of increasing W outweighs the effect of smaller σ'(x). The activations are saturated, so they hardly change. The net result is that the gradients explode.
For gain factors smaller than 1, the weight gradients neither explode nor vanish. This is because for small inputs, the tanh function is near zero and its derivative is near 1. In this regime the tanh function behaves like a linear activation, so as before the activations vanish but the weight gradients remain constant.
Sigmoid activation functions, by contrast, have vanishing gradients except when the gain factor is very large, in which case the gradients explode. Once again, the reason for this is more complicated than you might think.
For large inputs, the sigmoid function saturates towards 0 and 1, while for small inputs the sigmoid function remains near 0.5. So sigmoid functions prevent both exploding and vanishing activations, which allows the weight gradients to explode or vanish at high and low gain factors. In addition, the derivative of the sigmoid function is smaller than tanh (except when the inputs are large), with a maximum value of 0.25. These two effects combine in the figure above to produce vanishing gradients for a gain factor below about 10, and exploding gradients for larger gain factors.
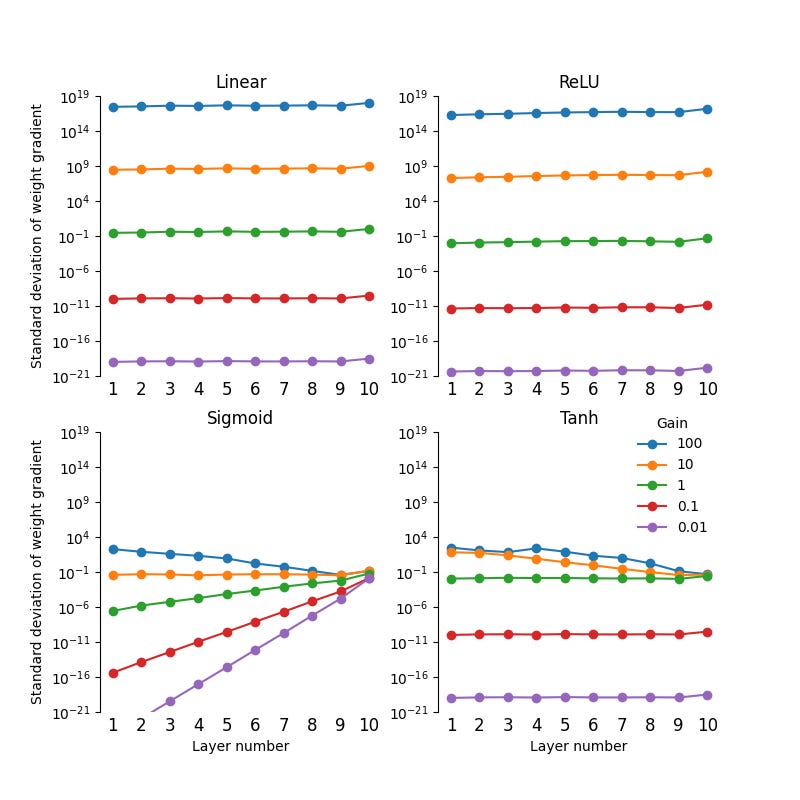
I’ve plotted the standard deviation of the bias gradients below. As we can see, tanh activations reduce the rate at which the bias gradients explode, but they do still explode for a gain factor greater than 1.
Are exploding activations harmful?
If exploding and vanishing activations don’t cause exploding gradients, then are they even a problem? To test, I ran another simple experiment.
The details of this experiment are the same as the first experiment, with two differences. First, I removed the biases. Second, instead of computing only the initial gradient, I trained the network on the MNIST dataset using SGD for 5 epochs. I chose the learning rate so that the scale of the initial parameter update ||ΔW||/||W|| is the same for each value of the gain factor. The code can be found here.
The key here is that the gradients neither explode nor vanish, but the activations do. Thus, we’re isolating for the effect of exploding or vanishing activations on neural network performance.
The loss and accuracy curves for each value of the gain factor are shown below. As we can see, exploding activations (due to large initial weights) harm learning, while vanishing activations (due to small initial weights) completely prevent it.
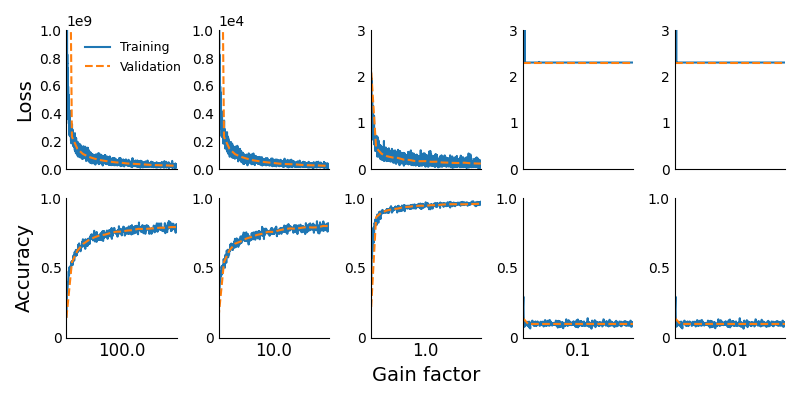
But what is it about exploding and vanishing activations that makes them harmful? And why are vanishing activations worse than exploding activations?
One plausible explanation might be that tanh and sigmoid activation functions saturate for large inputs and are approximately linear for small inputs, making learning difficult when activations are too large or too small.
But this doesn’t explain why exploding or vanishing activations would be a problem with ReLU, which doesn’t saturate and remains non-linear for small inputs. An alternative explanation is needed.
As we’ll see, in a ReLU network exploding and vanishing activations aren’t inherently harmful. What is harmful is when activations explode or vanish in the output layer of the network.
Why exploding activations in the output layer are harmful
To isolate for the effect of exploding and vanishing activations except in the output layer, I ran the same experiment except with the output activations (i.e., logits) normalized by the gain factor (to the power of L).3 The code can be found here.
The loss and accuracy curves are shown below. These are identical for all values of the gain factor. This reveals that in a ReLU MLP exploding and vanishing activations have no effect on learning, so long as neither the gradients nor the output layer activations explode or vanish.
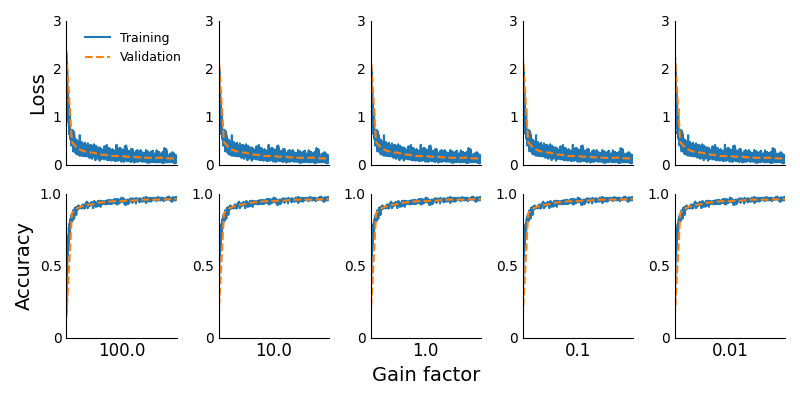
The problem with output activations that explode or vanish is that they are given as input to a loss function. And the loss functions we use in machine learning typically work best when their inputs have a variance that is neither very large nor very small.
Consider, for example, the softmax cross-entropy loss used in classification. The gradient of this loss with respect to the logits is (ŷ - y), where ŷ is the softmax output and y is a one-hot vector corresponding to the labels. If the variance of the logits is significantly larger than one, then ŷ approaches a one-hot vector, so the logit gradient (ŷ - y) is sparse with at most 2 non-zero elements. This slows down learning compared to when the variance is close to one and the logit gradient (ŷ - y) is dense.
Likewise, if the variance of the logits is significantly smaller than 1, then ŷ approaches a constant vector where each element is one divided by the number of classes. In that case, the logit gradient (ŷ - y) is a constant vector in all but one element. This not only slows down learning, but in the above experiments eventually led to an instability in training except when the learning rate was very small.4
I don’t have a great explanation for why vanishing activations seem to be worse than exploding activations for the softmax cross-entropy loss function. My best guess would be that having only one non-constant element in the logit gradient leads to worse performance than having two. But if there's anything we’ve learned from this post, it's that intuitive-sounding, hand-wavy explanations aren’t always correct.5
In this post, I mostly focus on the gradient with respect to the initial parameters. In principal, the gradients might not explode or vanish at the first iteration, but somehow the parameters might evolve in such a way that they lead to exploding or vanishing gradients after many iterations. However, in my experiments I found that this did not happen, even during instabilities in training.
For both the softmax cross-entropy loss and the mean squared error (MSE) loss, the gradient of the loss with respect to the final activation hL is given by (ŷ - y). For the cross-entropy loss, ŷ is the softmax output. In this case, (ŷ - y) scales independently of ||W||. For the MSE loss, (ŷ - y) = (hL - y) which can scale with ||W|| and L. Thus, the scaling of the weight gradient will be different for the MSE loss than for the cross-entropy loss. In both cases, however, the weight gradient scales independently of ℓ.
This is mathematically equivalent to changing the temperature of the softmax.
The training instabilities for gain factors of 0.1 and 0.01 in the above experiments were caused not by exploding gradients, which grow in space, but (as shown here) by gradients which grow in time. I use the term ‘gradient instability’ to refer to this type of growth.
Another common misconception is that gradient clipping prevents exploding gradients. Gradient clipping can be used when gradients grow exponentially in space (exploding gradients), but it can also be used to prevent gradients from growing exponentially in time (gradient instability). Gradient clipping prevents both types of gradient growth.
You may be wondering why there are so many myths and misconceptions about exploding gradients. I see two reasons. First, people rarely distinguish between the gradients with respect to the parameters and the gradients with respect to the activations, even though they can behave very differently. Second, the term is often used colloquially in a way that is different from its technical definition. In this post, we’ve seen four ways that gradients can grow or shrink:
Exploding/vanishing gradients: gradients that grow or shrink between layers.
Gradient instability: gradients that grow or shrink between training iterations.
Floating-point exceptions: includes numerical overflow, underflow, and NaNs.
Large/small gradients: these need not vary in space and/or time.
To minimize confusion, I encourage people to avoid using these terms interchangeably.